最近在补 XGP 中的最终幻想13-2时，遇到一个时钟谜题，感觉挺有意思，就像尝试用搜索算法将其解决。

问题描述

如下图所示，有一个时钟，包含个结点，每个节点有一个数字标识，玩家最开始可以任意选择一个结点，选择后，该结点被消除且指针会指向该结点的位置，根据该节点的数字值 n 分裂为两根指针分别向顺时针方向和逆时针方向旋转 n 个的单位长度。此后每次玩家只能选择指针指向的结点，选择结点后结点被消除，两指针合并指向选择结点的位置并按上述描述进行分裂和旋转，玩家需要将所有节点消除才能胜利。

注：玩家无法选择已经被消除的结点，若分裂旋转后的两指针均位于已被消除的结点位置，则判定游戏失败。

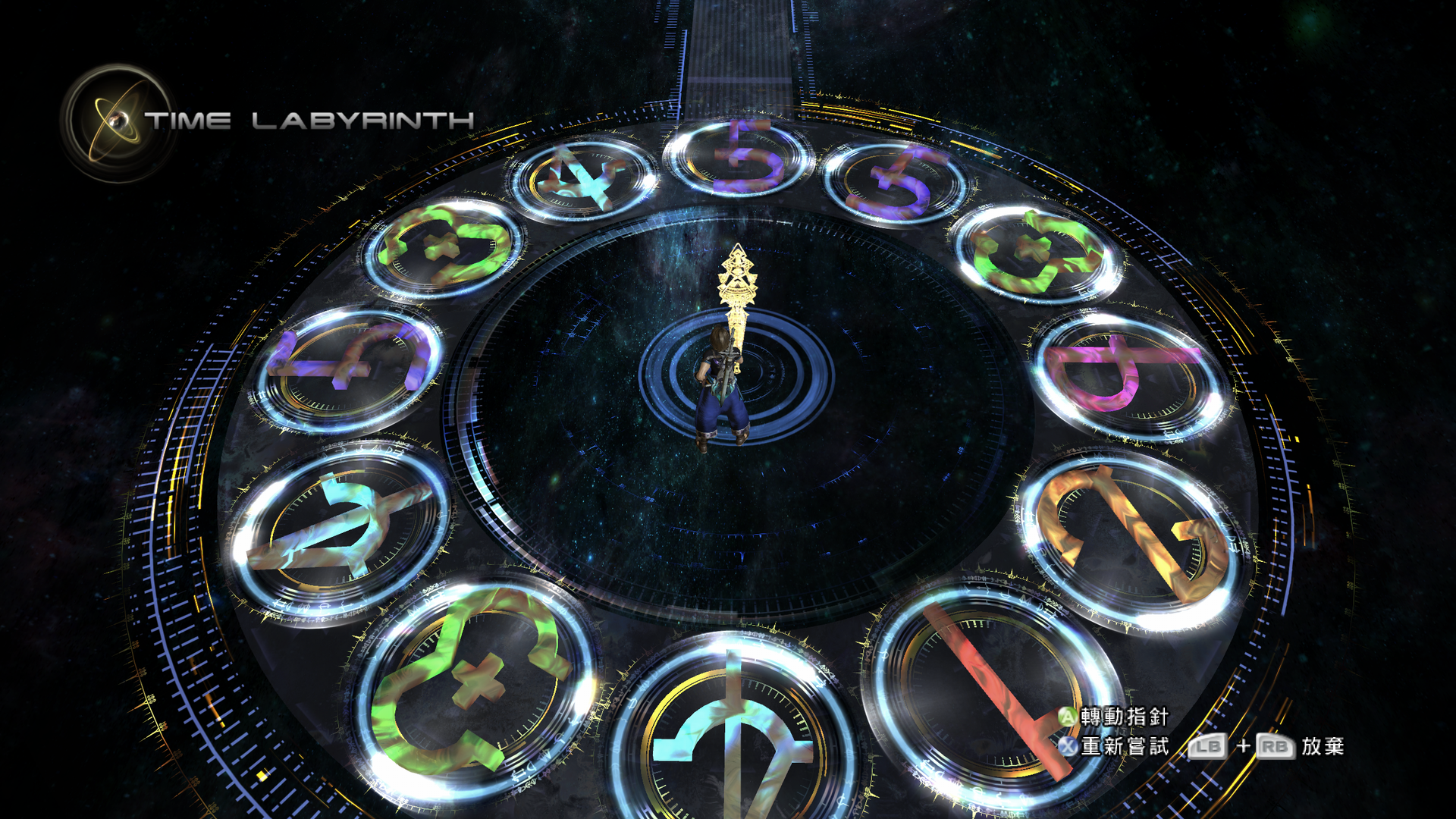
算法思路

本问题很容易想到利用深度优先搜索来解决，选择一个结点作为开始，如第一次选择 12 点钟位置的结点，（以下为了方便，按结点在时钟中排布位置 n 称作结点 n）该结点值为 5，则选中后分别向顺时针和逆时针方向旋转到达结点 5 和结点 7，这就产生了两个分支（相当于二叉树的左右子树），分别选择这两个结点继续搜索，若结点到达了一个已被访问过的结点（即该结点已被消除），则终止该方向上的搜索，并进行回溯，将路径上的该结点删除，并将访问标志复原。

若路径上的结点个数已经达到 12，即所有节点均被成功消除，则该路径为一个解路径，将该结果保存并回溯继续进行搜索，直到尝试了所有可能性，算法结束。

完整代码

#include<iostream>
#include<vector>
using namespace std;

class Solution {
private:
    int n;
    vector<int> path; // 搜索路径
    vector<vector<int>> res; // 成功路径
    void dfs(vector<int>& sequences, vector<bool>& visited, int ind) {
        if (visited[ind]) { // 已访问过
            return;
        }
        path.emplace_back(ind);
        visited[ind] = true;

        if (path.size() == n) { // 成功访问所有元素
            res.emplace_back(path);
        }

        int p1 = (ind - sequences[ind] + n) % n; // 逆时针方向旋转后的下标
        int p2 = (ind + sequences[ind]) % n; // 顺时针方向旋转后的下标

        if (p1 == p2) {
            dfs(sequences, visited, p1);
        }
        else {
            dfs(sequences, visited, p1);
            dfs(sequences, visited, p2);
        }

        // 回溯
        path.pop_back();
        visited[ind] = false;
    }
public:
    vector<vector<int>> clockPuzzle(vector<int>& sequences) {
        n = sequences.size();
        vector<bool> visited;
        for (int i = 0; i < n; ++i) { // 选取一个结点作为开始结点
            visited.assign(n, false); // 重置visited数组 
            dfs(sequences, visited, i);
        }
        return res;
    }
};

int main() {
    Solution S;
    vector<int> sequences = { 5,5,3,6,2,1,4,3,4,5,3,4 };
    auto res = S.clockPuzzle(sequences);
    for (const auto& re : res) {
        for (const auto& r : re) {
            cout << r << " ";
        }
        cout << endl << endl;
    }
}