《General overview of AMD SEV-SNP and Intel TDX》中文翻译
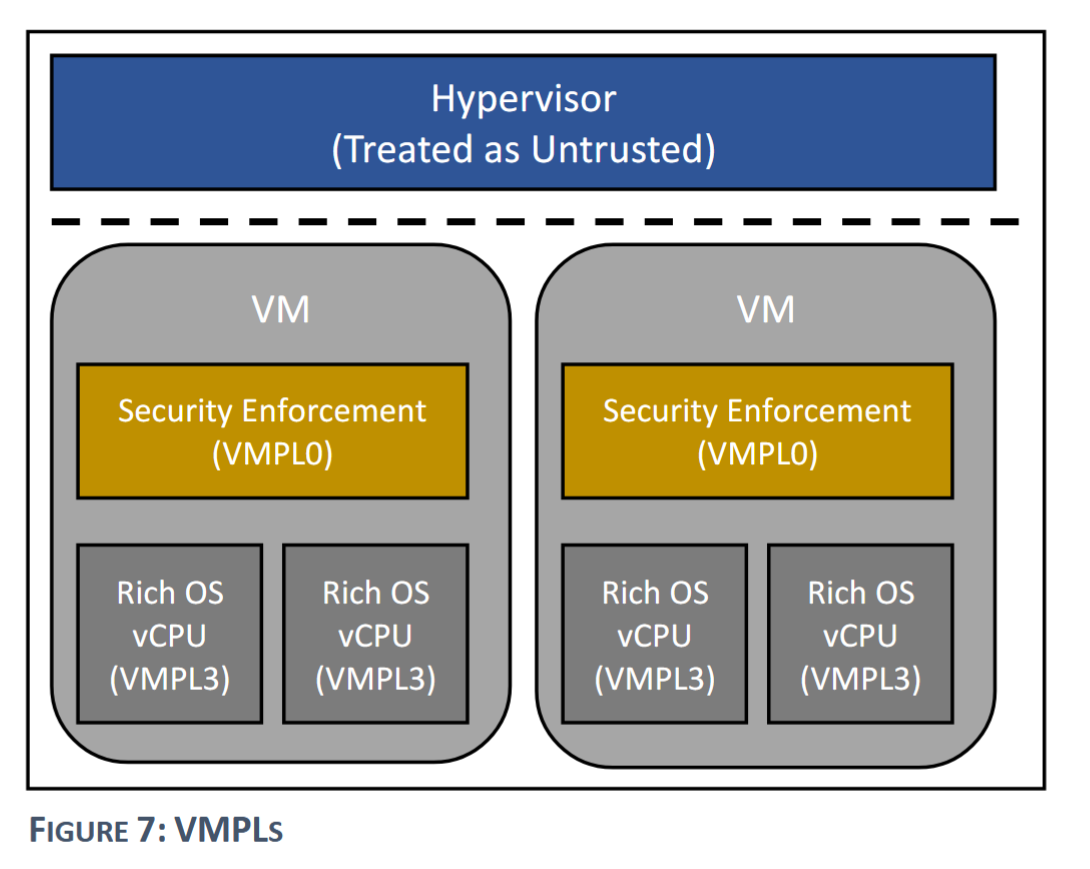
本文为论文《General overview of AMD SEV-SNP and Intel TDX》的中文翻译,翻译工具使用大模型 DeepSeek v3 和通义千问 2.5,经过了本人的核对与校正。由于本人在机密计算领域还处在初学阶段,因此一些专有名词的翻译可能存在问题,欢迎指出。 AMD SEV-SNP 和 Intel TDX 的总体概述 作者:Kevin Kollenda 摘要 可信执行环境(TEEs)在安全关键代码的执行上应用越来越普遍。AMD SEV-SNP 和 Intel TDX 是新开发的硬件扩展,旨在为虚拟机提供可信执行的环境。通过提供额外的完整性保证并基于之前的安全扩展,它们使得在云环境中实现不会危及敏感用户数据的机密计算成为可能。本文介绍了用于实现这些重大安全增益的额外组件和流程。 关键词 可信计算,AMD SEV-SNP,Intel TDX,安全嵌套分页 介绍如今,软件公司正越来越多地将其应用程序迁移到云环境中,而不是在本地托管。这可能会对机密用户数据构成风险,因为云服务提供商(CSP)可以直接访问运行潜在安全关键应用程序的硬件。...
将D盘空间划分给C盘
前段时间换了刚刚换了新的机械革命的笔记本,发现拿到手时磁盘已经预先分好了区,但是 C 盘(系统盘)只分了 200 GB。在装了 WSL 等一些必备的环境后,就只剩下不到 100 GB,感觉很没有安全感(😩),于是就想办法给 C 盘划分更多的空间,以下是一些经验分享。 尝试使用系统自带工具首先,我尝试着使用 Windows 自带的磁盘管理工具(Windows 11 下右键底部的“开始”键)。 开始的设想是:首先对 D 盘进行“压缩卷”将一部分空闲的存储空间转为“未分配”状态,然后对 C 盘执行”扩展卷“将刚腾出来的”未分配“空间给合并。但是发现 C 盘的”扩展卷“选项是灰色的,不可选。查阅资料得知一个磁盘在进行扩展卷时只能合并与之相邻的磁盘分区,而”压缩卷“腾出的空闲空间是位于磁盘右侧的,该空间无法与 C 盘进行合并,只能重新合入 D 盘中。 借助第三方工具要想使得 C 盘能够合并 D 盘的空闲空间,就必须使得 D 盘划分出的空闲空间位于 D 盘的左侧,而这必然涉及到磁盘数据的移动,存在数据丢失的风险,Windows 也并没有提供这样的功能。 于是转而寻求第三方工具的帮助,最...
《最终幻想7:重生》体验分享
《最终幻想7:重生》是我 2024 年最期待的游戏之一。由于发售时还没有 PS5,加上考研复试等事务缠身,没能第一时间体验。后来,后面为了剧情体验的连贯性,我又重温了一遍四年前的《最终幻想7:重制版》,直到最近两个月才正式开坑。 历经 87 小时通关一周目后,内心感慨万千,不吐不快,于是便有了这篇体验分享。整体而言,《最终幻想7:重生》无愧于我 2024 年的年度游戏,甚至在 jrpg 品类中几乎稳坐我心中的头把交椅。但它并非完美,其中仍有一些让我不太满意或感到遗憾的地方,接下来便一一细说。 提示:本文存在剧透内容。 广阔,未必自由相较于重制版第一作,《重生》最大的进化便是引入了一个可供探索的大地图。但请注意,尽管游戏的地图很大,我却很难称之为“开放世界”。实际上,游戏并未表现出什么构建一个生动、真实的奇幻世界的意图,而是通过一个个清单项来构成世界。而这势必会导致游戏体验上的重复,制作组为了缓解这种枯燥感,尽可能地在这些重复的清单项中引入了差异化设计。例如,同样是捕获陆行鸟,不同地区有不同的解决方式,这些在一定程度上确实减轻了重复感。 支线任务方面,相比上一作,《重生》有了显...
CSAPP Malloc Lab
本 Lab 需要实现一个内存分配器,技巧性较强,对应知识点为书中的第 9 章的第 9.9 节。个人认为是所有 Lab 中难度最高的一个,我这里也是时间所迫,只参照教材实现了隐式空闲链表,显式空闲链表的实现尚存在一些 bug,在本文暂不介绍。 思路实验要求实现 mm_init, mm_malloc, mm_free, mm_realloc。 mm_malloc 需要返回 8 字节对齐的指针。 mm_realloc: 返回一个指向至少 size 字节的内存区域指针。 如果 ptr 为空,作用等同于 mm_malloc(size)。 如果 size 等于 0,作用等用于 mm_free(ptr)。 如果 ptr 非空,将 ptr 指向区域的大小更改为 size 字节,并返回新区域的内存地址。 隐式空闲链表首先介绍一下书中介绍的隐式空闲链表的设计,主要分为两个方面:空闲块的设计和空闲链表的组织。 空闲块的设计 一个空闲块由三部分组成:首部、载荷(可能包含填充)和尾部。头部和尾部的内容完全一致,之所以要引入这样的冗余信息,是为了实现常数时间复杂度的反向访问。因为内存载荷大小的不确定性...
CSAPP Shell Lab
本 Lab 需要实现一个简易的 shell,主要考察对进程和信号的理解,以及对与其相关的 POSIX API 的使用,对应知识点为书中的第 8 章内容。 思路实验要求实现一个简单的 shell,要求支持如下特性: 输入 ctrl-c 触发 SIGINT 信号,输入 ctrl-z 触发 SIGTSTP 信号,发送给给前台运行的任务和依赖于这些任务的子任务(子进程)。 如果命令行以 & 结尾,那么本次作业将被置于后台运行,否则置于前台运行。 每个作业可以通过 PID(process id)或 JID(job id)来指定,其中 JID 需要加上前缀 %。 支持下列内建命令: quit:终止 shell 的运行。 jobs:列出所有的后台作业。 bg <job>:重启 <job>(PID 或者 JID),通过发出 SIGCONT 信号,然后将其运行在后台。 fg <job>:重启 <job>(PID 或者 JID),通过发出 SIGCONT 信号,然后将其运行在前台。 回收所有的僵尸进程。 命令行解释执行eval 函数的...
CSAPP Cache Lab
本 Lab 主要考察对计算机高速缓存(Cache)机制的理解,以及如何针对 Cache 进行程序的优化,对应知识点为书中的 6.4 ~ 6.6 节内容。 Part A: Writing a Cache Simulator思路基本流程Part A 需要实现一个 Cache 模拟器,能够根据 valgrind 工具所生成的访存跟踪数据,模拟在特定参数的 Cache 环境下的命中(hits)次数、不命中(misses)次数和置换(evictions)次数,目标是实现与 csim-ref 同等的功能。模拟器需要具备的几个功能模块如下: 对命令行参数进行参数解析。 读取 trace 文件并解析为地址访问流。 定义 Cache 模拟器数据结构,以及相关的函数操作,包括初始化和地址访问。 遍历解析出来的地址访问流,依次进行访问模拟,计算得到命中次数等信息。 接下来分别对它们进行介绍。 命令行参数解析根据实验手册的提示,可以使用 getopt 函数进行命令行参数的解析。另外,如果需要支持长选项(形如 --opt arg),则可以使用 GNU C 库提供的扩展版本 getopt_lo...
2024开源操作系统训练营 rCore Chapter8练习
编程作业思路本实验要求为死锁和信号量机制实现死锁检测功能,并提供系统调用 enable_deadlock_detect,用以开启和关闭死锁检测功能。在开启死锁检测功能的情况下,用户使用 mutex_lock 或 semaphore_down 尝试获取互斥资源时,如果发现系统处于不安全状态(可能发生死锁)时拒绝对应的资源获取请求。 实验手册中介绍的死锁检测算法为银行家算法(Banker\’s Algorithm),由 Dijkstra 提出,算法的流程可以参照手册,这里不再详细介绍,代码实现如下: 123456789101112131415161718192021222324252627282930313233343536/// Banker's Algoritm for dead lock checkfn deadlock_check(available: Vec<usize>, allocation: Vec<Vec<usize>>, need: Vec<Vec<usize>>) -> bool ...
2024开源操作系统训练营 rCore Chapter6练习
编程作业思路linkat本实验需要实现 3 个与文件系统相关的系统调用,首先是用来创建文件硬链接的 linkat. 首先介绍一下什么是硬链接,硬链接作为一种抽象概念,可以看作指向一个文件实体的指针,类似于 C++ 中的智能指针 shared_ptr。而从内核代码的角度来看,硬链接在文件系统中的实体就是 文件目录项 。每个硬链接对应一个目录项,这个目录项指向一个相同的索引节点(inode),每个 inode 存储了文件的实际数据块(的指针)及其元数据(文件大小、文件类型等)。 由于 rCore 的文件系统被简化为单级目录(只包含根目录),因此实现 linkat 的思路就很清晰了:根据文件名 old_name 查找其对应的 inode,获取 inode_id 并将引用计数加一,创建一个新的目录项 (new_name, inode_id),将其插入根目录的数据段末尾。 需要注意的是,rCore 文件系统的 inode 分为虚拟文件系统层的 Inode 和在持久化设备(硬盘)上实际存储的 DistInode,可以通过 Inode 所实现的 read_disk_inode 和 modify...
2024开源操作系统训练营 rCore Chapter5练习
编程作业思路进程创建如果只是想根据特定程序来创建进程,而不需要 fork + exec 组合提供的灵活性(如文件重定位等),那么 spawn 将是一个更简洁且效率更高的选择,本实验要求便是实现它。 对于 spawn 的实现,确实可以简单地将 fork 和 exec 拼接起来。但需要注意的是,fork 首先拷贝父进程的地址空间,exec 再将该地址空间替换,二者融合后最开始地址空间的拷贝其实是徒劳的。如以下代码所示: 123let memory_set = MemorySet::from_existed_user(&parent_inner.memory_set); // futile code!...let (memory_set, user_sp, entry_point) = MemorySet::from_elf(elf_data); stride 调度算法实现一个简单的步长调度算法,由于算法思路比较简单,这里直接介绍实现方式。 首先,为了保存进程的“步长”和优先级信息,需要为进程控制块添加两个字段 stride 和 prio(不考虑性能,为了实现的简单,pass...
2024开源操作系统训练营 rCore Chapter4练习
编程作业思路重写 sys_get_time 和 sys_task_info首先,第一个任务:由于引入了虚拟内存后,sys_get_time 和 sys_task_info 失效了,需要进行重写。 这里解释一下为什么会失效:以 sys_get_time 为例,用户在发起系统调用时,传入的参数 _ts 是用户态下的虚拟地址,它需要借助内核的软件地址转换机制,查找任务对应的页表,将 _ts 转换为物理地址,再对该地址处的值进行填充。这里可以使用 page_table.rs 中预先实现好的 translated_byte_buffer,它将一整个虚拟地址段翻译为一系列的物理地址段(每页一段),这样如果结构体 TimeVal 和 TaskInfo 横跨多个页面也同样适用。 注意,内核态代码中的地址仍然是虚拟地址,只不过在 rCore 中,内核态的低 256GB 为直接映射,因此好像内核代码在直接访问物理地址,其实还是虚拟地址。 实现 mmapPOSIX 标准中的 mmap 是将一个文件或其他对象的数据映射到进程的地址空间中,而本实验需实现的 mmap 则为简化版本,只是简单地向进程地址...