高效的LeetCode二叉树本地IDE调试方案
在 LeetCode 刷题过程中，有时候遇到一些难以难以直接观察出来的错误，此时通常想要利用单步调试来解决，但奈何只有 LeetCode Plus 会员才可以使用其网页的调试功能。好在绝大部分本地 IDE 都具备十分强大的调试功能，我们只需要将自己的解题代码复制到本地，并编写简单的测试程序即可。但是对于二叉树相关的题，测试数据的编写显得不那么容易，本文编写了一个匹配 LeetCode 题目中的二叉树定义的类，该类包含一些基本的静态函数，能够很方便地实现二叉树的构造和二叉树的遍历。 LeetCode 二叉树的序列表示方式LeetCode 中针对二叉树的输入数据以一个层序遍历序列的形式给出。与通常我们所说的层序序列不同的是，该层序序列包含从根节点到最后一个非空结点之间的所有空结点，该空结点以 null 的标识符给出，以此保证根据此序列所构造二叉树的唯一性（单纯依靠常规的不含空结点的层序序列无法构造一棵唯一的二叉树）。以下是一个简单的例子： 输入： root = [3, 9, 20, null, null, 15, 7] 带构造与遍历的二叉树类为了方便能在本地 IDE 中直接根据输入...
二分搜索的几种写法与常见问题
最近在比赛和刷题的时候经常遇到二分答案的题，但时不时会因为一些细节上的错误而浪费时间，本文旨在整理常见的二分搜索的写法、二分搜索可能会遇到的一些小问题，以及 C++ 中与二分搜索相关的库函数，以免今后再犯类似的错误。 二分搜索的写法查找某个值的下标定义函数 binarySearch(nums, target) 为搜索有序数组 nums 中是否存在 i 使得 nums[i] == target，如果是，返回 i，否则返回 -1. 12345678910111213141516int binarySearch(vector<int>& nums, int target) { int low = 0, high = (int)nums.size() - 1; while (low <= high) { int mid = low + (high - low) / 2; if (nums[mid] == target) { return mid; } else if (nums[mid] > target...
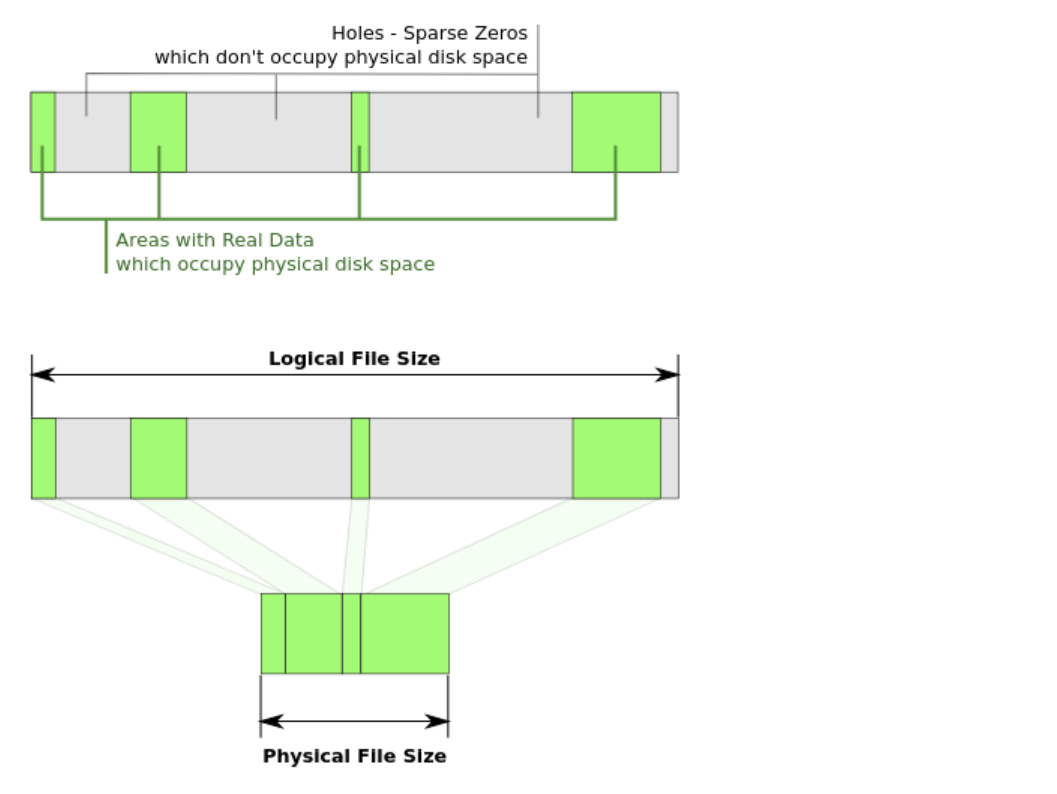
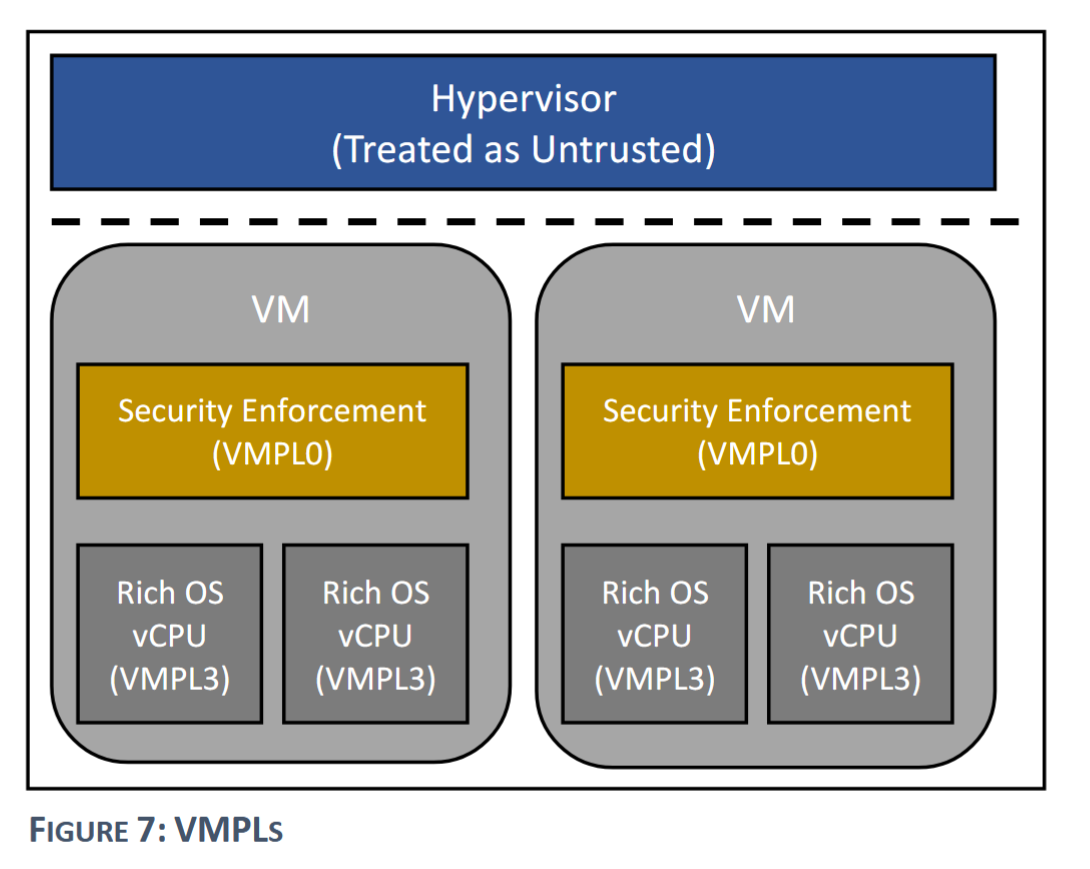
算法分析与设计编程题 回溯法
装载问题题目描述 解题代码递归回溯1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950// goods[i]表示货物i的重量, c1,c2分别表示货船1和货船2的载重量vector<vector<int>> optimalLoading(vector<int>& goods, int c1, int c2) { int n = goods.size(); // 货物数量 int maxSum = 0; // 当前最大载货量 // curSelection[i]表示货物i是否放入货船1中（true表示放入） vector<bool> curSelection(n, false); // optimSelection记录maxSum对应的货物存放方式 vector<bool> optimSelection; // 递归搜索函数 function<void(int, int)...
算法分析与设计编程题 贪心算法
活动安排问题题目描述 解题代码12345678910111213141516171819vector<bool> greedySelector(vector<vector<int>>& intervals) { int n = intervals.size(); // 将活动区间按结束时间的从小到大排序 auto cmp = [](vector<int>& interval1, vector<int>& interval2) { return interval1[1] < interval2[1]; }; sort(intervals.begin(), intervals.end(), cmp); vector<bool> res(n, false); // 结束时间最早的活动必定位于某个最优解之中 int minStart = intervals[0][1]; res[0] = ...
算法分析与设计编程题 动态规划
矩阵连乘题目描述 解题代码12345678910111213141516171819202122232425262728293031323334353637void printOptimalParens(vector<vector<int>>& partition, int i, int j) { if (i == j) cout << "A" << i; // 单个矩阵，无需划分 else { cout << "("; printOptimalParens(partition, i, partition[i][j]); printOptimalParens(partition, partition[i][j] + 1, j); cout << ")"; }}// nums[i]: nums[0]为矩阵A1的行数，nums[i](i >= 1)表示矩阵Ai的列数// 如输入为 nums ...
算法分析与设计编程题 递归与分治策略
棋盘覆盖题目描述 解题代码123456789101112131415161718192021222324252627282930313233343536373839404142// para: 棋盘，行偏移，列偏移，特殊行，特殊列void dividedCovering(vector<vector<int>>& chessBoard, int dr, int dc, int sr, int sc, int size) { if (size == 1) return; size /= 2; // 划分为四部分 if (sr < dr + size && sc < dc + size) { // 特殊点位于左上部分 divideCovering(chessBoard, dr, dc, sr, sc, size); } else { int nr = dr + size - 1, nc = dc + size - 1; // 新覆盖点 chessBoard[nr][nc] = 1...
常见排序算法
插入排序直接插入123456789void insertSort(vector<int>& nums) { for (int i = 1; i < nums.size(); ++i) { int j = i; while (j >= 1 && nums[j] < nums[j - 1]) { swap(nums[j], nums[j - 1]); --j; } }} 折半插入12345678910111213141516171819void binaryInsertSort(vector<int>& nums) { for (int i = 1; i < nums.size(); ++i) { int key = nums[i]; int low = 0, high = i - 1; while (low <= high) { int mid = low + (high - low)...
数据结构编程题 查找
二叉树定义以下为本文解题代码的二叉树定义。 123456struct TreeNode { int val; TreeNode* left, *right; TreeNode(int val = 0, TreeNode* left = nullptr, TreeNode* right = nullptr) : val(val), left(left), right(right) {}}; 递归二分查找题目描述写出二分查找的递归算法。初始调用时，left 为1，right 为 n. 解题代码1234567891011bool recurBS(vector<int>& nums, int target, int left, int right) { if (left > right) return false; int mid = (left + right) / 2; if (nums[mid] == target) return true; else if (nums[mid] > target)...
数据结构编程题 图
图定义邻接表1234567891011121314struct ArcNode { // 边结点 int verIdx, weight; ArcNode* next; ArcNode(int verIdx, int weight, ArcNode* next) : verIdx(verIdx), weight(weight), next(next) {}};struct VNode { // 顶点结点 char vertex; ArcNode* first;};struct AlGraph { vector<VNode> VNodes;}; 邻接矩阵1234struct MGraph { vector<char> vertices; // 顶点集 vector<vector<int>> edges; // 邻接矩阵}; 邻接表转邻接矩阵题目描述写出从图的邻接表转化为邻接矩阵的算法。 解题代码1234567891011121314151...
数据结构编程题 二叉树
二叉树定义以下为本文解题代码的二叉树定义。 123456struct TreeNode { int val; TreeNode* left, *right; TreeNode(int val = 0, TreeNode* left = nullptr, TreeNode* right = nullptr) : val(val), left(left), right(right) {}}; 非递归先序遍历题目描述编写先序遍历二叉树的非递归算法。 解题代码12345678910111213141516void nonRecurPre(TreeNode* root) { if (root == nullptr) return; stack<TreeNode*> s; while (root != nullptr || !s.empty()) { if (root != nullptr) { cout << root->val << " "; s...
